Sistem bilangan ini mempunyai radix atau bisa juga disebut basis yang digunakan sebagai nilai patokan. Terdiri atas 4 sistem bilangan yaitu sistem bilangan biner, desimal, oktal, dan heksadesimal dengan radix yang berbeda dalam setiap bilangan. Di bawah ini merupakan tabel berisi jenis-jenis sistem bilangan beserta radix dan simbol yang digunakan untuk setiap sistem bilangan.

Sistem bilangan desimal
Di sistem bilangan desimal, cara menghitung bilangannya dengan menggunakan 10 simbol, yakni ‘0’, ‘1’ ,’2′ ,’3′, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, dan ‘9’. Bilangan desimal mempunyai radix atau basis 10. Jika kita punya angka 678, maka angka 8 tersebut disebut satuan, angka 7 disebut puluhan, dan angka 6 disebut ratusan.
Angka yang memiliki arti terbesar, dalam contoh tersebut yakni angka yang bernilai ratusan, yang mempunyai letak paling kiri dinamakan Most Significant Bit (MSB). Dalam bilangan tersebut yang dinamakan MSB adalah angka 6. Dan untuk angka yang memiliki nilai terkecil, dalam contoh bernilai satuan, dan mempunyai letak paling kanan dinamakan Least Significant Bit (LSB) dalam bilangan tersebut yaitu angka 8.
Sistem bilangan biner
Dalam sistem bilangan biner, menggunakan 2 simbol, yakni ‘1’ dan ‘0’. Oleh karena itu, biner mempunyai radix 2. Contoh bilangan biner adalah 1100. dalam hal ini, angka 1 paling kiri merupakan MSB dan angka 0 paling kanan adalah LSB.
Sistem bilangan oktal
Sistem bilangan oktal mempunyai radix 8. jadi simbol yang digunanakan juga 8 yaitu ‘0’, ‘1’ ,’2′ ,’3′, ‘4’, ‘5’, ‘6’ dan ‘7’. Bilangan ini digunakan sebagai alternatif untuk menyederhanakan sistem pengkodean biner. Karena 8=23, sehingga 1 digit oktal dapat mewakili 3 digit biner. Contoh bilangan oktal adalah 476. Angka 4 merupakan MSB dan angka 6 merupakan LSB.
Sistem bilangan heksadesimal
Heksadesimal menggunakan 16 simbol, yakni ‘0’, ‘1’ ,’2′ ,’3′, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’, ‘A’, ‘B’, ‘C’, ‘D’, ‘E’, dan ‘F’. Oleh karena itu heksadesimal mempunyai radix 16. Bilangan heksadesimal juga digunakan untuk alternatif dalam penyederhanaan sistem pengkodean biner. Hal ini dikarenakan 16=24, sehingga 1 digit heksadesimal dapat mewakili 4 digit biner.
Konversi sistem bilangan
Konversi bilangan desimal
Desimal -> Biner
Cara yang digunakan adalah dengan membagi bilangan desimal secara berturut-turut dengan pembagi radix biner yang mana adalah 2. Sisa pembagian bilangan tersebut akan bernilai 0 atau 1. Sisa awal pembagian menunjukkan LSB yang nanti diletakkan di sisi paling kanan dan hasil akhir dari pembagian menunjukkan MSB yang diletakkan di sisi paling kiri.

Angka 25 dibagi dengan 2 yang merupakan radix dari biner dan mempunyai hasil 12 dengan sisa pembagian 1, angka 1 tersebut merupakan LSB. Lalu 12 dibagi lagi dengan 2 dan menghasilkan 6 dengan sisa 0. Pembagian tersebut dilakukan berulang sampai bilangannya tidak bisa dibagi lagi dengan 2. Dan MSB untuk contoh tersebut adalah 1. Sehingga mempunyai hasil akhir 110012 .
Untuk menandakan bilangan tersebut desimal, diberi angka 10 pada bagian bawah kanan bilangan tersebut. 10 ini menunjukkan radix bilangan. Hal ini juga berlaku untuk penulisan setiap sistem bilangan untuk memudahkan kita dalam mengidentifikasi jenis dari sistem bilangan tersebut.
Desimal -> Oktal
Bilangan desimal yang akan diubah dibagi dengan 8 yang merupakan radix dari bilangan oktal. Sisa pembagian tersebut dicatat. Dibagi secara berturut-turut serta sisa awal pembagian menunjukkan LSB dan sisa akhir pembagian menunjukkan MSB.

Angka 25 dibagi dengan 8 yang merupakan radix dari oktal dan mempunyai hasil 3 dengan sisa 1. Angka 3 sudah tidak bisa dibagi dengan 8 sehingga LSB dalam perhitungan ini adalah 1 dan untuk MSB nya 3. Dan hasil konversinya adalah 31.
Desimal -> Heksadesimal
Bilangan desimal dibagi secara berturut-turut dengan 16 yang merupakan radix dari bilangan heksadesimal. Sisa pembagian tersebut dicatat serta sisa awal pembagian menunjukkan LSB dan sisa akhir pembagian menunjukkan MSB.

Angka 25 dibagi dengan 16 yang merupakan radix dari heksadesimal dan mempunyai hasil 1 dengan sisa pembagian 9. Bilangan 1 sudah tidak bisa dibagi dengan 16. Sehingga hasil konversinya adalah 19.
Konversi bilangan biner
Biner -> Desimal
Salah satu cara yang bisa digunakan untuk mengkonversikan bilangan biner menjadi bilangan desimal dengan cara menjumlahkan hasil perkalian tiap digit bilangan biner dengan angka 2 yang mempunyai pangkat koefisien biner yang mana setiap digit tersebut mempunyai ekuivalen yang berbeda sesuai pada tabel.


Ada 7 digit biner yang hasil perkalian dari setiap digitnya sudah dijumlahkan dan mendapatkan hasil 75.
Biner -> Oktal
Konversi dilakukan dengan cara mengelompokkan setiap 3 digit bilangan biner dimulai dari sebelah kanan. Setiap kelompok akan diubah ke dalam bilangan oktal.


Setiap digit bilangan oktal mempunyai ekivalen yang berbeda sesuai dengan tabel. Digit paling kiri menyisakan 1, agar tidak bingung, depan angka 1 bisa ditambah 0 agar kelompok tersebut berisi tiga digit bilangan biner. Setelah itu bisa diubah ke bilangan oktal disesuaikan dengan ekivalen biner 3 yang sesuai pada tabel.
Biner -> Heksadesimal
Dilakukan dengan cara mengelompokkan setiap 4 digit bilangan biner dimulai dari sebelah kanan. Setelah itu, setiap kelompok tersebut akan diubah ke dalam bilangan heksadesimal.


Sama seperti konversi bilangan biner ke oktal, dalam contoh ini digit paling kiri menyisakan 100 yang mana hanya tiga digit sedangkan untuk syarat harus dikelompokkan menjadi 4 digit. Angka sebelum 1 bisa diberi 0 agar memenuhi 4 digit. Setelah itu bisa diubah ke heksadesimal dengan mencocokkan ekivalen di tabel.
Konversi bilangan oktal
Oktal -> Desimal
Setiap digit di oktal juga mempunyai bobot berbeda terhadap ekivalensi dalam desimal seperti yang ditunjukkan dalam tabel di bawah ini.


Bilangan oktal dikonversi dengan menjumlahkan bobot kali nilai dari setiap posisi. 7 dikali dengan 81 dan mempunyai hasil 56 lalu dijumlah dengan hasil perkalian 0 dengan 80 yang mempunyai hasil 0. Sehingga hasil konversinya 56.
Oktal -> Biner
Konversi dilakukan dengan cara mengubah setiap digit menjadi ekivalen biner 3 digit, sesuai dengan ekivalensi tiap digit yang sudah diterangkan pada tabel ekivalen digit oktal dengan biner 3.
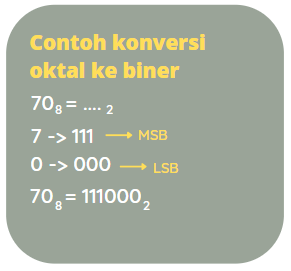
Oktal -> Heksadesimal
Konversi bilangan oktal ke heksadesimal dilakukan dengan merubah bilangan oktal menjadi bilangan desimal terlebih dahulu atau bisa juga diubah ke bilangan biner. Setelah itu, bilangan tersebut baru dikonversi ke bilangan heksadesimal.


Konversi bilangan heksadesimal
Heksadesimal -> Desimal
Konversi bilangan dari heksadesimal ke desimal dikonversi dengan mengkalikan setiap digit bilangan heksadesimal dengan bobot nilai dari masing-masing posisi.


E sama dengan 14 dalam sistem bilangan heksadesimal. Sehingga 1 dikali 162 , 4 dikali dengan 161 dan 14 dikali dengan 160 lalu hasil dari perkalian tersebut dijumlahkan dan mempunyai hasil akhir 334.
Heksadesimal -> Biner
Dikonversi dengan cara mengubah setiap digit bilangan heksadesimal menjadi ekivalen biner 4 bit. Untuk ekivalen tersebut bisa dilihat pada tabel ekivalen digit heksadesimal dengan biner 4 yang sudah dijelaskan sebelumnya.

Perhitungan tersebut mempunyai hasil akhir 000101001110 atau bisa juga ditulis dengan menghilangkan nol di depan sehingga menjadi 101001110 untuk mempersingkat, cara penulisan dengan menghilangkan nol di depan tidak akan merubah nilai dari bilangan tersebut.
Heksadesimal -> Oktal
Sama seperti konversi oktal ke heksadesimal, konversi heksadesimal ke oktal juga harus diubah ke bilangan biner atau desimal terlebih dahulu. Setelah itu baru diubah ke oktal.






